Programação Linear para Otimizar Sistemas de Produção
A solução ótima para determinada cadeia de produção raramente é encontrada implicitamente pelo “achômetro”. Situações onde é necessário determinar o menor custo e/ou maior lucro para determinada cadeia de produção exigem modelos matemáticos precisos, tal como representa o método Simplex. É possível ainda criar aplicações para auxiliar a tomada de decisão de gestores nas cadeias de produção.
O caso enunciado
O objetivo de determinada fábrica é minimizar o custo total de produção e ainda atender as restrições nutricionais dos cardápios. Para o Cardápio A, há a necessidade de compôr uma dieta de 3 mg de Vitamina A, 8 mg de Proteína e 9 mg de Lipídeos. Já
para o Cardápio B são necessários para os mesmos componentes 6, 5 e 4 mgs respectivamente. Sabe-se que a necessidade mínima de Vitamina A, Proteínas e Lipídeos são de 29, 33 e 43 miligramas respectivamente, e os
custos operacionais para a montagem dos cardápios estão vinculados à R$0,94 para o Cardápio A e R$1,38 para o Cardápio B.
As variáveis de decisão para produção
Conceitualmente, as variáveis de decisão são os itens de produção: neste caso, os Cardápios A e B.
As restrições de capacidade e demanda
Os recursos disponíveis para produção, quantitativamente limitados: neste caso, Vitamina A, Proteína e Lipídeos.
A solução gráfica bidimensional
Compreende pontos que representam produções ótimas das variáveis de decisão: neste caso, produziremos X unidades do Cardápio A e Y unidades do Cardápio B. Reforçando que, cada cardápio possui suas restrições mínimas de nutrientes para produção.
O ponto ótimo
Um ponto específico na solução gráfica bidimensional representa a relação perfeita de produção de cada cardápio para minimizar o custo de produção. Por exemplo: produzimos 150 unidades do Cardápio A, e 350 unidades do cardápio B, ou nenhuma unidade do Cardápio B e vice-versa.
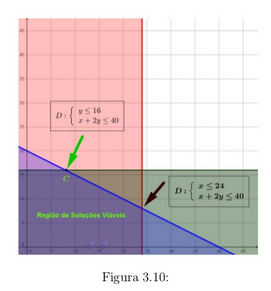
GLPK – solução ótima via Simplex
A biblioteca gratuita GLPK, disponível para iOS, Linux e Windows, está disponível, junto a exemplos de scripts para soluções em MathProg. Ela soluciona problemas matemáticos por meio de algoritmos pré-configurados, nos quais é possível fornecer parâmetros e obter os resultados possíveis rapidamente.
Aplicações podem ser desenvolvidas com Simplex / Programação Linear
É possível criar aplicações para monitorar o fluxo de produção e emitir notificações de alerta sobre produção fora da média ótima, produzindo gráficos e permitindo que os gestores tomem decisões baseadas nos gráficos gerados, em tempo real.
Literatura disponível
Se você está habituado com modelos matemáticos, este material pode ser de grande utilidade:
Se optar por livros reconhecidos, estes atendem:

O conteudo foi útil? Isso é fantástico. Quer incentivar mais posts como esse? Mostre seu apoio com qualquer valor.
Chave PIX: d0311e58-cb6e-4d47-b3d8-3d4254763ce7















[…] seja, seu servidor tem uso médio de 20 horas/mês, e você nem precisa de Planejamento de Carga ou Otimização de Sistemas de Produção pra chegar nesse […]
[…] seja, seu servidor tem uso médio de 20 horas/mês, e você nem precisa de Planejamento de Carga ou Otimização de Sistemas de Produção pra chegar nesse número. Agora você sabe a capacidade necessária e só precisa fazer uma […]